ブログ・お知らせ
【算数と数学】計算ミスをなくすには?
- 06_受験関連,算数・数学
先日、小学1年生の方から、こんな質問を頂きました。
「計算ミスって、どうやったらなくなるんですか?」
「計算ミスって、どうやったらなくなるんですか?」
まずは、その問題意識を持てていることが素晴らしいと思います。
そして、この質問に対する私の答えはこれです。
そして、この質問に対する私の答えはこれです。
「「6+7」「6+8」の答えに注意すること。」
これだけです。
何故か。
全ての理由が分かった、という方は、この先は読まれなくて結構です。
「足し算は分かったが、引き算や掛け算の場合は?」と思われた方は、
足し算の説明を飛ばして、読んでいただければと思います。
さて、では、理由を説明しましょう。
計算が難しくなるのは「繰上りが発生する時」です。
そして、計算ミスが発生するのは、「しっかり計算を覚えられていない場合」です。
これを前提に、場合分けして考えます。
① 繰り上がらない計算
例:1+4,3+5,8+1…
例:1+4,3+5,8+1…
これは、ほとんどミスすることはありませんね。
ここで間違える場合は、指を使ってでも、しっかり答えを確認すれば、まず間違えません。
ここで間違える場合は、指を使ってでも、しっかり答えを確認すれば、まず間違えません。
② 繰り上がる計算
a.足して10になる計算
例:1+9,2+8,3+7.4+6,5+5
a.足して10になる計算
例:1+9,2+8,3+7.4+6,5+5
全部書き出してみました(逆順は省略)。
これら「足して10になる」計算も間違えることはないでしょう。
これら「足して10になる」計算も間違えることはないでしょう。
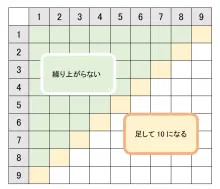
b.5との足し算
例:5+6,5+7,5+8,5+9
繰り上がらない足し算、足して10は省略しました。
これも、計算は難しくありませんね。
これも、計算は難しくありませんね。
c.同じ数同士の足し算
例;6+6,7+7,8+8,9+9
例;6+6,7+7,8+8,9+9
これも、掛け算を覚えるまでもなく、覚えやすい答えになりますね。
d.9との足し算
例:9+6,9+7,9+8
例:9+6,9+7,9+8
9との足し算も、仕組みになれると難しくありません。
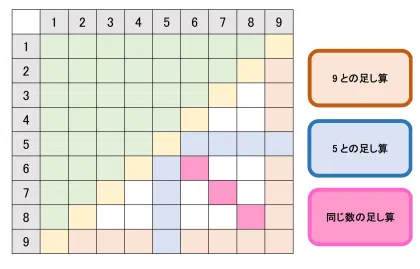
さぁ、ここまでくると、残ったのは、
3+8,4+7,4+8
6+7,6+8,7+8
の6つです。
e.足して12,15になる
例:4+8,7+8
例:4+8,7+8
足して12,15というのは、覚えやすい計算なので覚えてしまいましょう。
f.足して11になる
例:3+8,4+7
これも覚えてしまいましょう、なのですが、ここでミスする、という方もあるかもしれません。
その場合は、これらの計算も、「間違えやすい計算」として注意する、という形を取りましょう。
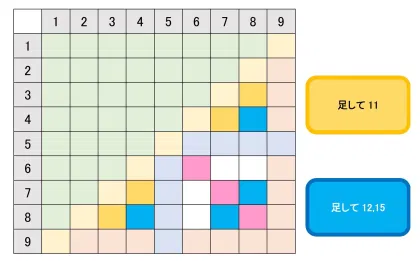
となると、計算が難しい=ミスをしやすいのは、
6+7,6+8
の二つに絞り込めます。
(人によっては3+8,4+7を加えた四つ)
ですから、この答えをしっかり覚え、
この計算が出た時には注意するようにすれば、
足し算のミスはなくなる、というわけです。
実は「ミスをしやすいところ」というのは、こうやって絞り込むことが出来るのです。
「「6+7」と「6+8」さえ覚えれば良い」は結論ですが、
ここに至る、ミスの原因を絞り込む過程こそが大事です。
いったん、計算システムさえ頭に入れて計算をしてみれば、
どんな計算の場合でも、「自分がミスしやすいところ」は解析可能なのです。
足し算を例にしましたが、引き算の場合でも、九九の場合でも、同様の絞り込みをしてみましょう。
また、数学に進んでも、その個人がどこで間違えているか調べてみましょう。
これで、計算ミスを大幅に減らすことが出来ます。
そして、この絞り込みには、もう一つの意味があります。
それは、計算方法を整理し、はっきりさせることで、
「「自分がミスしやすいところ」以外のミス」を減らすことが出来る、ということです。
つまり、いままで漫然と計算していた、「5や9との足し算」「繰上りのない足し算」「足して11」といった計算も、この分類を意識して計算することで、これまで無意識で計算していた部分が意識化され、ミスが減るわけです。
本人による見直しにしても、先生によるミスの指摘にしても、
漫然と見たり指摘したりするだけでは、
本人が犯しているミスの本質にたどりつきません。
この部分を意識化しないと、同じミスを何度も繰り返す結果になります。
自動で問題生成してくれるタブレットでも、
自分で間違いのループの理由に気付けなければ、
「また計算ミスです」と、同じ問題が繰り返され続けるのです。
今後、塾における問題生成は、ある程度まで(特に計算問題は)AIによる自動出力が主流になってくるでしょう。
しかし、こういう、間違いの本質まで本人と共に気付くことが出来る能力については、まだまだ人間の方が上かな、と思います。
(…いや、まぁ、低レベルな先生だと既にAIに負けてらっしゃる方もいらっしゃるかもしれませんが。)
(…いや、まぁ、低レベルな先生だと既にAIに負けてらっしゃる方もいらっしゃるかもしれませんが。)
「彼を知り己を知れば百戦殆うからず」
自分の弱点をしっかりと把握して、計算ミスをなくしましょう!
- 意識化,簡単,計算ミス,計算ミスのなくしかた,算数,自己分析,数学,彼を知り己を知れば百戦殆うからず
オススメ記事
-
- お知らせ
-
- お知らせ
-
- 03_自由研究,算数・数学